Sécurisation des communications

Programme

Généralités

Un peu d'histoire

Voici les premières méthodes de chiffrement (source Wikipédia) :

Le plus vieux document chiffré
Le premier « document » chiffré connu remonte à l'Antiquité. Il s'agit d'une tablette d'argile, retrouvée en Irak, et datant du xvi^e siècle av. J.-C. Un potier y avait gravé sa recette secrète en supprimant des consonnes et en modifiant l'orthographe des mots.
La technique grecque
Entre le X^e et le VII^e siècle av. J.-C. semble attestée une technique de chiffrement par transposition, c'est-à-dire reposant sur le changement de position des lettres dans le message, en utilisant un bâton de diamètre déterminé appelé scytale. On enroulait en hélice une bande de cuir autour de la scytale avant d'y inscrire un message. Une fois déroulé, le message était envoyé au destinataire qui possédait un bâton identique, nécessaire au déchiffrement.
Nabuchodonosor
Aux alentours de -600, Nabuchodonosor, roi de Babylone, employait une méthode originale : il écrivait sur le crâne rasé de ses esclaves, attendait que leurs cheveux aient repoussé, et il les envoyait à ses généraux. Il suffisait ensuite de raser à nouveau le messager pour lire le texte. Il s'agit toutefois de stéganographie à proprement parler et non pas de cryptographie : l'information est cachée et non pas codée.
En utilisant cette technique, l'interception du message par un tiers est tout de suite remarquée.
La technique des Hébreux
À partir du ve siècle av. J.-C., l'une des premières techniques de chiffrement est utilisée dans les textes religieux par les Hébreux qui connaissent plusieurs procédés.
Le plus connu appelé Atbash est une méthode de substitution alphabétique inversée.
Elle consiste à remplacer chaque lettre du texte en clair par une autre lettre de l'alphabet choisie de la manière suivante : A devient Z, B devient Y, etc.
Les premiers « vrais » systèmes de cryptographie
Il faut attendre -200 pour voir apparaître les premiers « vrais » systèmes de cryptographie. Ce sont essentiellement des chiffrements par substitution

Il existe 3 types de substitutions :
- monoalphabétique : remplace chaque lettre du message par une autre lettre de l'alphabet ;
- polyalphabétique : utilise une suite de chiffres monoalphabétiques (la clé) réutilisée périodiquement ;
- polygrammes : substitue un groupe de caractères dans le message par un autre groupe de caractères.

Le code de César
Le code de César est la méthode cryptographique, par substitution monoalphabétique, la plus ancienne (ier siècle av. J.-C.).
Cette méthode est utilisée dans l'armée romaine, la faible alphabétisation de la population la rend suffisamment efficace.
Son système est simple, il consiste à remplacer une lettre par celle obtenu dans l'alphabet par un décalage (circulaire) de n rang.

Attention vocabulaire

Chiffrer : il s’agit de rendre un document illisible avec une clef de chiffrement
Déchiffrer : il s’agit de rendre lisible un document chiffré, en ayant connaissance de la clef de chiffrement
Crypter : cela n’existe pas
Décrypter : il s’agit de rendre lisible un document chiffré, sans avoir connaissance de la clef de chiffrement
Cryptologie : il s’agit de la science du secret

Le chiffrement par substitution ou par transposition

Définition

Un chiffrement par substitution est un chiffrement où chaque lettre du texte clair est remplacé par un autre caractère.
Lors d'un chiffrement par substitution simple ou monoalphabétique, l'alphabet est remplacé par un autre.

Cas où le remplacement est lié à un simple décalage dans l'ordre alphabétique :

Si je souhaite chiffrer NSI, je cherche la correspondance des lettres dans l'alphabet décalé :
N -> O
S -> T
I -> J
NSI est donc chiffré en OTJ

Cas d'une substitution plus complexe :

Si je souhaite chiffrer NSI, je cherche la correspondance des lettres dans l'alphabet de substitution :
N -> W
S -> T
I -> V
NSI est donc chiffré en WTV

On souhaite décrypter un message qui a été chiffré par substitution en décalant simplement l'alphabet usuel :

Combien de tentatives au maximum devrez vous faire ?
Conclure sur la sécurité d'un tel protocole.

Vous devez décrypter le message suivant: JL AFWL KL JVKL ZL JYHXBL MHJPSLTLUA

On souhaite décrypter un message qui a été chiffré par substitution:

Combien de tentative au maximum devrez vous faire.
Conclure sur la sécurité d'un tel protocole.

Bien que le code par substitution semble inviolable, ce n'est pas le cas, il est même assez facile à craquer.
Et c'est assez facile à comprendre, regardez le message chiffré si dessous:
QV NV IVGLFIMV HLFEVMG VM XOZHHV
On remarque que la lettre V revient très souvent, il s'agit donc probablement d'un E.
En effet en analysant la fréquence d'apparition des lettres dans une langue, on peut rapidement déchiffrer le message qui était ici : JE ME RETOURNE SOUVENT EN CLASSE

Le chiffrement Atbash

L'Atbash est un chiffrement par substitution monoalphabétique simple pour l'alphabet hébreu. Cette méthode de chiffrement substitue א à ת, ב à ש, et ainsi de suite, inversant l'alphabet. Cette méthode de chiffrement est faible car il s'agit d'une simple substitution monoalphabétique.

Écrire une fonction atbash qui recevra en paramètre une chaine de caractères ch,et qui chiffrera cette chaîne. Ainsi, les A deviennent des Z, les B des Y, ...
En testant votre fonction avec "BONJOUR", vous devez obtenir "YLMQLFI".

Vous pouvez utiliser la méthode find(), qui renvoie l'index de la première occurrence rencontrée, ou -1 si la valeur n'est pas trouvée.
Si besoin vous pouvez tester le code suivant:

txt = "hello world"
x = txt.find("o")
print(x)

Modifier votre fonction atbash afin que la chaîne de caractère en paramètre puisse contenir des espaces.

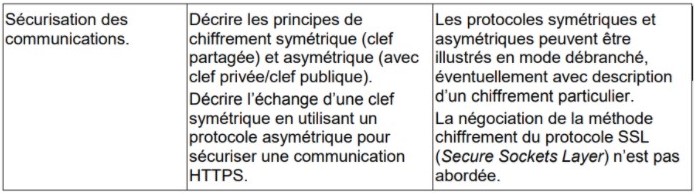
Le chiffrement de César

Le chiffrement César est basé sur un décalage de l'alphabet. Cependant pour chaque message les mots ont le même déplacement.

Nous allons chiffrer HELLO WORD avec un décalage de 3

Lettre	Lettre décalée
A	D
B	E
C	F
...	...
X	A
Y	B
Z	C

HELLO WORD ce transforme en KHOOR ZRUOG.

Chiffrez la phrase "IL AIME LA SPECIALITE NSI" à l'aide du code de César et en utilisant un décalage de 5.

Cryptographie

la fonction chr()

Pour cet exercice nous allons utiliser la fonction chr de Python qui prend en argument un entier (codé en décimal) et qui renvoie le caractère ASCII associé.

Voici une table ASCII qui associe à chaque nombre entier compris entre 0 et 255 son écriture dans différentes bases et surtout son caractère ASCII :

Décimal   Octal   Hex  Binaire   Caractère
-------   -----   ---  --------    ------
000      000    00   00000000      NUL    (Null char.)
001      001    01   00000001      SOH    (Start of Header)
002      002    02   00000010      STX    (Start of Text)
003      003    03   00000011      ETX    (End of Text)
004      004    04   00000100      EOT    (End of Transmission)
005      005    05   00000101      ENQ    (Enquiry)
006      006    06   00000110      ACK    (Acknowledgment)
007      007    07   00000111      BEL    (Bell)
008      010    08   00001000       BS    (Backspace)
009      011    09   00001001       HT    (Horizontal Tab)
010      012    0A   00001010       LF    (Line Feed)
011      013    0B   00001011       VT    (Vertical Tab)
012      014    0C   00001100       FF    (Form Feed)
013      015    0D   00001101       CR    (Carriage Return)
014      016    0E   00001110       SO    (Shift Out)
015      017    0F   00001111       SI    (Shift In)
016      020    10   00010000      DLE    (Data Link Escape)
017      021    11   00010001      DC1    (XON)(Device Control 1)
018      022    12   00010010      DC2    (Device Control 2)
019      023    13   00010011      DC3    (XOFF)(Device Control 3)
020      024    14   00010100      DC4    (Device Control 4)
021      025    15   00010101      NAK    (Negative Acknowledgement)
022      026    16   00010110      SYN    (Synchronous Idle)
023      027    17   00010111      ETB    (End of Trans. Block)
024      030    18   00011000      CAN    (Cancel)
025      031    19   00011001       EM    (End of Medium)
026      032    1A   00011010      SUB    (Substitute)
027      033    1B   00011011      ESC    (Escape)
028      034    1C   00011100       FS    (File Separator)
029      035    1D   00011101       GS    (Group Separator)
030      036    1E   00011110       RS    (Request to Send)(Record Separator)
031      037    1F   00011111       US    (Unit Separator)
032      040    20   00100000       SP    (Space)
033      041    21   00100001        !    (exclamation mark)
034      042    22   00100010        "    (double quote)
035      043    23   00100011        #    (number sign)
036      044    24   00100100        $    (dollar sign)
037      045    25   00100101        %    (percent)
038      046    26   00100110        &    (ampersand)
039      047    27   00100111        '    (single quote)
040      050    28   00101000        (    (left opening parenthesis)
041      051    29   00101001        )    (right closing parenthesis)
042      052    2A   00101010        *    (asterisk)
043      053    2B   00101011        +    (plus)
044      054    2C   00101100        ,    (comma)
045      055    2D   00101101        -    (minus or dash)
046      056    2E   00101110        .    (dot)
047      057    2F   00101111        /    (forward slash)
048      060    30   00110000        0
049      061    31   00110001        1
050      062    32   00110010        2
051      063    33   00110011        3
052      064    34   00110100        4
053      065    35   00110101        5
054      066    36   00110110        6
055      067    37   00110111        7
056      070    38   00111000        8
057      071    39   00111001        9
058      072    3A   00111010        :    (colon)
059      073    3B   00111011        ;    (semi-colon)
060      074    3C   00111100        <    (less than sign)
061      075    3D   00111101        =    (equal sign)
062      076    3E   00111110        >    (greater than sign)
063      077    3F   00111111        ?    (question mark)
064      100    40   01000000        @    (AT symbol)
065      101    41   01000001        A
066      102    42   01000010        B
067      103    43   01000011        C
068      104    44   01000100        D
069      105    45   01000101        E
070      106    46   01000110        F
071      107    47   01000111        G
072      110    48   01001000        H
073      111    49   01001001        I
074      112    4A   01001010        J
075      113    4B   01001011        K
076      114    4C   01001100        L
077      115    4D   01001101        M
078      116    4E   01001110        N
079      117    4F   01001111        O
080      120    50   01010000        P
081      121    51   01010001        Q
082      122    52   01010010        R
083      123    53   01010011        S
084      124    54   01010100        T
085      125    55   01010101        U
086      126    56   01010110        V
087      127    57   01010111        W
088      130    58   01011000        X
089      131    59   01011001        Y
090      132    5A   01011010        Z
091      133    5B   01011011        [    (left opening bracket)
092      134    5C   01011100        \    (back slash)
093      135    5D   01011101        ]    (right closing bracket)
094      136    5E   01011110        ^    (caret circumflex)
095      137    5F   01011111        _    (underscore)
096      140    60   01100000        `
097      141    61   01100001        a
098      142    62   01100010        b
099      143    63   01100011        c
100      144    64   01100100        d
101      145    65   01100101        e
102      146    66   01100110        f
103      147    67   01100111        g
104      150    68   01101000        h
105      151    69   01101001        i
106      152    6A   01101010        j
107      153    6B   01101011        k
108      154    6C   01101100        l
109      155    6D   01101101        m
110      156    6E   01101110        n
111      157    6F   01101111        o
112      160    70   01110000        p
113      161    71   01110001        q
114      162    72   01110010        r
115      163    73   01110011        s
116      164    74   01110100        t
117      165    75   01110101        u
118      166    76   01110110        v
119      167    77   01110111        w
120      170    78   01111000        x
121      171    79   01111001        y
122      172    7A   01111010        z
123      173    7B   01111011        {    (left opening brace)
124      174    7C   01111100        |    (vertical bar)
125      175    7D   01111101        }    (right closing brace)
126      176    7E   01111110        ~    (tilde)
127      177    7F   01111111      DEL    (delete)

Quels sont les entiers qui code l'alphabet en lettre capitale?
Quels scripts faut-il écrire pour obtenir l'affichage de la lettre A et du mot NSI ?

Écrire le script Python qui permet d'obtenir une structure de données de type dict qui doit être :

{'A': 0, 'B': 1, 'C': 2, 'D': 3, 'E': 4, 'F': 5, 'G': 6, 'H': 7, 'I': 8,
'J': 9, 'K': 10, 'L': 11, 'M': 12, 'N': 13, 'O': 14, 'P': 15, 'Q': 16, 'R': 17, 
'S': 18, 'T': 19, 'U': 20, 'V': 21, 'W': 22, 'X': 23, 'Y': 24, 'Z': 25}

Le chiffrement de César

Méthode :
À chaque lettre de l'alphabet on associe un nombre de à 0 à 25.
On ajoute à ce nombre un nombre choisi, par exemple 7.
Le reste de la division euclidienne du nombre obtenue par 26 correspond au chiffre qui codera la lettre initiale.

Exemple :
La lettre Y est associée à 24 ; on lui ajoute 7 on obtient 31.
Le reste de la division euclidienne de 31 par 26 est 5. Ce qui donne F.
Y est donc codé par F.

Quels scripts écrire pour obtenir le code de la lettre A et du mot NSI avec un décalage de 17.
Rappelez vous que le reste de la vision euclidienne de a par b s'obtient en Python ainsi : a%b
Quel script écrire pour obtenir le dictionnaire de la table de codage/décodage de l'alphabet avec la méthode du chiffrement de César avec un décalage de 17 ?
On stockera ce dictionnaire dans une variable nommée d.
Vous devez obtenir le dictionnaire suivant :
```
{'A': 'R', 'B': 'S', 'C': 'T', 'D': 'U', 'E': 'V', 'F': 'W', 'G': 'X', 'H': 'Y', 'I': 'Z',
 'J': 'A', 'K': 'B', 'L': 'C', 'M': 'D', 'N': 'E', 'O': 'F', 'P': 'G', 'Q': 'H', 'R': 'I',
 'S': 'J', 'T': 'K', 'U': 'L', 'V': 'M', 'W': 'N', 'X': 'O', 'Y': 'P', 'Z': 'Q'}
```
Utiliser la fonction str aussi bien pour les clés que pour les valeurs.

Une fonction de codage
1. Reprendre votre dictionnaire d et tester :
```
d['A']
d['V']
d['E']
```
2. Dans le script précédent quel est le statut de 'A', 'V' et 'E' ? Clé ou valeur ?
3. Écrire une fonction en Python codage(mot) qui prend en argument un chaîne de caractère mot écrit en lettre capitale et qui renvoie le mot codé par le chiffrement de César de décalage 17.

Une fonction de décodage
1. On suppose que le décalage reste de 17.
  Utiliser le dictionnaire d pour créer un dictionnaire dic_rev qui permettra de décoder : ce dictionnaire associera à chaque lettre majuscule chiffrée la lettre correspondante dans le message initial en clair.
  Exemple : d['S'] correspond à 'J' donc dic_rev['J'] vaut 'S'.
2. Écrire une fonction en Python decodage qui prend en argument un chaîne de caractère chiffre correspondant au mot chiffré écrit en lettre capitale et qui renvoie le mot en clair initial, sachant que le chiffrement est lié au code César de décalage 17.

Chiffrement par transposition

Un chiffrement par transposition est un chiffrement dans lequel les caractères du message clair sont conservés mais où leur position dans le message a été modifiée.

"augmenter sa securite !" peut être chiffré par transposition en l'anagramme suivante "cause argumente et ris!".
Un tel exemple n'est pas simple à déchiffrer.

Pour faciliter le déchiffrage, le plus simple est de suivre un ordonnancement précis.
Par exemple, en lisant une lettre sur deux puis en reprenant dans l'ordre les lettres non lues, "TRANSPOSITIONPLUSSIMPLEADECHIFFRER" devient "TASOIINLSIPEDCIFERNPSTOPUSMLAEHFRR".

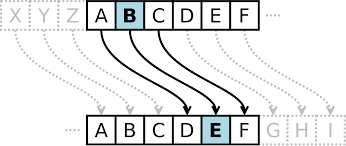
Le plus ancien dispositif militaire de cryptographie connu est la scytale spartiate. Cette technique remontant au Ve siècle avant notre ère, consiste en un bâton de bois autour duquel on enroulait une bande fine de sorte à recouvrir en grand partie le bâton. Sur la surface ainsi recouverte, il suffisait d'écrire le message à transmettre.
Le fait de dérouler le ruban conduisait à une transposition dans l'ordre des lettres lorsque l'on lisait directement sur le ruban.
Pour déchiffrer, il suffit d'enrouler le ruban sur un autre bâton de même largeur.
Par exemple, on écrit le texte "THESCTYALISATRANSPOSITIONCIPHER" sur un bâton :

Le ruban déroulé contient dans l'ordre de déroulement le texte chiffré "TNSEHCPIEIOSSPSACHITYETRTRIAAONL".

On considère le texte extrait du début de L'Énéide, poème en latin de Virgile : "ARMAVIRUMQUECANO".
On entre les lettres composant le texte dans un tableau 2D où chaque lettre appartient à une case :

clair = [["A", "R", "M", "A"], 
         ["V", "I", "R", "U"],
         ["M", "Q", "U", "E"],
         ["C", "A", "N", "O"]]

Écrire une fonction permuter_lignes qui prend en paramètres un tableau 2D comme clair ainsi que deux indices de ligne l1 et l2. Cette fonction doit conserver le tableau 2D saisi en argument et renvoyer un tableau dans lequel les lignes d'indice l1 et l2 ont été permutées.

Tester la fonction avec le tableau 2D clair. Vous devez obtenir pour les 3 affichages successifs suivant :

>>>print(clair)
[['A', 'R', 'M', 'A'], ['V', 'I', 'R', 'U'], ['M', 'Q', 'U', 'E'], ['C', 'A', 'N', 'O']]
>>>print(permuter_ligne(clair, 1, 3))
[['A', 'R', 'M', 'A'], ['C', 'A', 'N', 'O'], ['M', 'Q', 'U', 'E'], ['V', 'I', 'R', 'U']]
>>>print(clair)
[['A', 'R', 'M', 'A'], ['V', 'I', 'R', 'U'], ['M', 'Q', 'U', 'E'], ['C', 'A', 'N', 'O']]

Écrire une fonction permuter_colonnes qui prend en paramètres un tableau 2D comme clair ainsi que deux indices de colonne c1 et c2. Cette fonction doit renvoyer un tableau dans lequel les colonnes d'indice c1 et c2 ont été permutées. (peu importe ici que la tableau initial soit modifié ou non)

Tester la fonction avec le tableau 2D clair. Vous devez obtenir pour l'affichage suivant :

>>>print(permuter_colonne(clair, 1, 2))
[['A', 'M', 'R', 'A'], ['V', 'R', 'I', 'U'], ['M', 'U', 'Q', 'E'], ['C', 'N', 'A', 'O']]

On considère un tableau 2D formé de 4 lignes et 4 colonnes.
En voici un exemple :

clair = [["A", "R", "M", "A"], 
         ["V", "I", "R", "U"],
         ["M", "Q", "U", "E"],
         ["C", "A", "N", "O"]]

Proposer une fonction AESdecalage_dans_ligne qui prend en paramètre un tableau 2D seize formé de 4 lignes et 4 colonnes et qui renvoie un tableau de 2D dans lequel :

la première ligne est inchangée,
les éléments de la seconde ont été décalés de 1 rang vers la gauche (le premier devant aussi le dernier dans cette "permutation circulaire"),
les éléments de la troisième ont été décalés de 2 rangs vers la gauche par permutation circulaire,
les éléments de la dernière ont été décalés de 3 rangs vers la gauche par permutation circulaire.

Par exemple, AESdecalage_dans_ligne(clair) renvoie le tableau suivant :

clair = [["A", "R", "M", "A"], 
         ["I", "R", "U", "V"],
         ["U", "E", "M", "Q"],
         ["O", "C", "A", "N"]]

Le chiffrement symétrique

Généralités

Un chiffrement symétrique est un chiffrement ou la clé de chiffrement est la même pour chiffrer et déchiffrer le message. Cette clé unique doit être connue de l'émetteur et du récepteur du message.

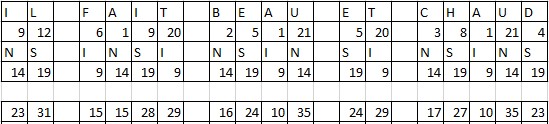
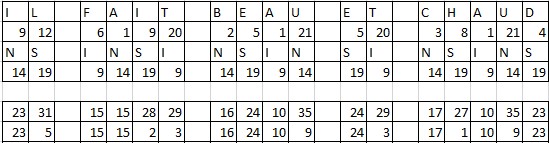
On souhaite réaliser le chiffrement symétrique de : "IL FAIT BEAU ET CHAUD", pour cela nous avons besoin d'une clé de chiffrement sous forme d'une chaîne de caractères, par exemple "NSI"

Étape 1: On écrit la clé sous le message et on la répète si besoin.
Étape 2: On écrit les indices de position des lettres.
Étape 3: On fait la somme des indices de position des lettres.
Étape 4: Si la valeur trouvée dépasse 26, on soustrait 26 pour recommencer au début de l'alphabet.
Étape 5: On cherche la nouvelle lettre avec l'indice de position trouvé.

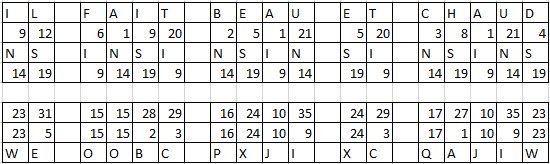
Détailler les étapes pour retrouver le message d'origine (=déchiffrer) en partant du message chiffré "WE OOBC PXJI XC QAJIW" obtenu dans l'exemple de chiffrement symétrique précédent.

Le chiffrement AES

Le chiffrement AES (Advanced Encryption Standard) est un algorithme de chiffrement/déchiffrement symétrique. Il permet la transmission d’un message confidentiel par une liaison non sécurisée.

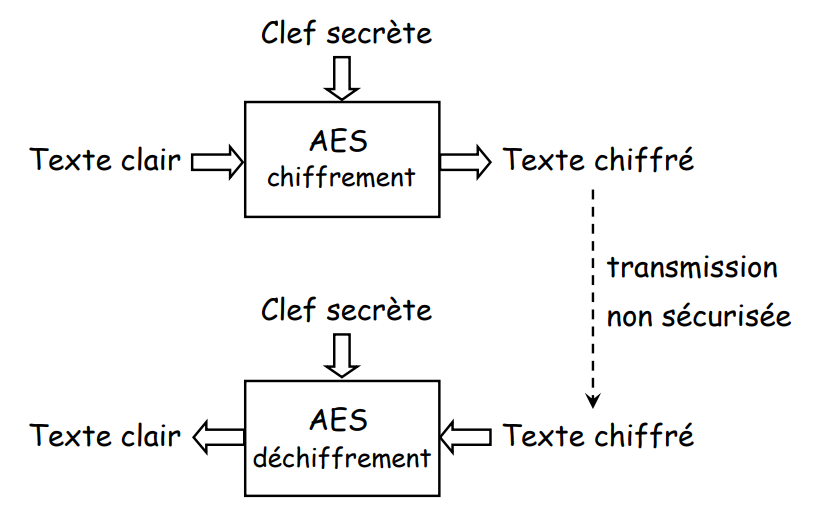
Une même clef secrète est utilisée pour les opérations de chiffrement et de déchiffrement (c’est un secret partagé entre l’expéditeur et le destinataire du message).
AES est un algorithme de chiffrement par blocs, les données sont traitées par blocs de 128 bits pour le texte clair et le chiffré. La clef secrète a une longueur de 128 bits, d’où le nom de version : AES 128 (il existe deux autres variantes dont la clef fait respectivement 192 et 256 bits).

La clé : un mot de passe qui permet de chiffrer le texte et ensuite de le déchiffrer. Sa taille va définir le nombre de tour que va subir le texte entre le moment où il n’est pas chiffré et le moment où il est chiffré.

Plus la clé est longue, plus il y aura de combinaisons différentes.

Voici un tableau des principales tailles de clé :

un tableau montrant le nombre de combinaisons selon la taille de la clé

Tout repose donc sur cette clé secrète de chiffrement qui ne doit jamais être divulguée, sinon on accède aux données chiffrées.

Des chercheurs disent qu’avec un trillion de machines, chacune pouvant tester un milliard de clés par seconde, cela prendrait plus de deux milliards d'années pour récupérer une clé AES 128 bits.

Le gouvernement américain dit même que « L'architecture et la longueur de toutes les tailles de clés de l'algorithme AES (128, 192 et 256) sont suffisantes pour protéger des documents classifiés jusqu'au niveau « SECRET ». Le niveau « TOP SECRET » nécessite des clés de 192 ou 256 bits. »

AES est implémenté dans des logiciels et du matériel à travers le monde pour chiffrer les données sensibles. On le trouve également pour le chiffrement de base de données ou de stockage de données. Par exemple, on utilise AES pour chiffrer un fichier ou disque dur ou le stockage de mot de passe comme les gestionnaires de mots de passe, la protection par mot de passe de fichiers PDF ou de fichiers ZIP. Les applications telles que WhatsApp, Signal, VeraCrypt ou 7-zip et WinZip utilisent AES pour chiffrer les communications ou le contenu.

Le chiffrement AES : un algorithme de chiffrement par bloc et on applique à ces derniers différentes opérations réitérées (une substitution, des décalages des éléments par ligne, des mélanges des données dans les colonnes, des additions "xor" avec une clé variable) pour obtenir des blocs de sorties.

En cryptographie, c’est le principe de réseau de permutation-substitution.

Vous pouvez visualiser les étapes du fonctionnement de ce chiffrement depuis ce site, les indications étant en anglais.

Il existe des sites qui permettent de chiffrer ou de déchiffrer avec le chiffrement AES sous peu que la clé de chiffrement soit donnée.
Ce site en est un.

Décrypter ce message en ligne grâce à une clé "monlyceenumerique : quel site !" en 128 bits :
"oKoDzhlhgBK3ODhc0tiHxeUA0WdB7HKJ8leDf5BdQKs="
De quel ouvrage s'agit-il ?

Quelle affirmation est fausse ?

Il est possible de chiffrer et de déchiffrer un message avec la même clé.
Le chiffrement AES est un chiffrement fiable qui permet de garder des données à l’abri.
Les tailles de clés les plus utilisées sont : 94, 128, 192 et 256 bits.
D'après la NSA, le chiffrement en 192 bits est suffisant pour sécuriser des fichiers classés « SECRET ».

Le chiffrement asymétrique

Nous venons de voir que le chiffrement symétrique nécessitait l’échange d’une clé au préalable, et qu’il y avait une seule et même clé pour chiffrer et déchiffrer. Désormais, nous allons nous intéresser au chiffrement asymétrique.

Le chiffrement asymétrique permet d'éviter le problème lié à l'échange sécurisé d'une clé secrète.
Le premier chiffrement asymétrique a été présenté publiquement en 1976 par Whitfield Diffie et à Martin Hellman.
L'algorithme RSA (acronyme tiré du nom de ses trois inventeurs Ronald Rivest, Adi Shamir et Leonard Adleman) a été présenté en 1978 et est considéré comme le premier algorithme concret basé sur un chiffrement asymétrique.

Bob possède deux clés :

une privée qu'il garde secrète (schématisé ci-dessous par une clé ),
une publique qui sera échangée avec le message (schématisé ici par un cadenas ).

Voici le fonctionnement de l'utilisation d'un chiffrement asymétrique pour qu'Alice puisse envoyer un message à Bob sans qu'un espion interceptant leurs communications ne puisse lire le message.

Bob envoie sa clé publique (ici un cadenas ouvert) à Alice. Évidemment, il garde cachée sa clé privée (celle qui permet d'ouvrir le cadenas).
Alice chiffre son message en utilisant la clé publique de Bob (schématiquement cela revient à mettre le message dans une boîte qu'Alice ferme à clef avec le cadenas reçu de Bob).
Alice peut le faire quand bien même elle ignore la clé privée de Bob (schématiquement, cela revient à dire qu'elle peut fermer le cadenas de Bob même si elle est incapable d'ouvrir ce cadenas).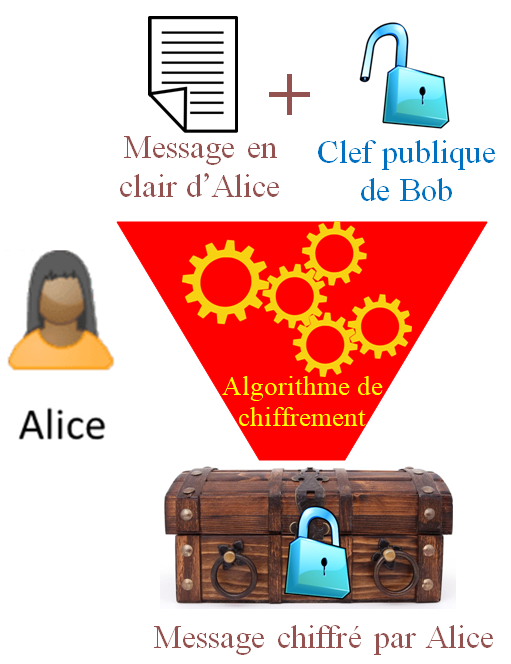
Alice envoie ensuite le message chiffré (schématiquement Alice envoie à Bob la boîte fermée à clé avec le cadenas de Bob).
Bob, peut avec sa clé privée déchiffrer le message reçu pour lire le message en clair d'Alice (schématiquement Bob ouvre la boîte fermée à clef par son cadenas en utilisant sa clé conservée secrètement).

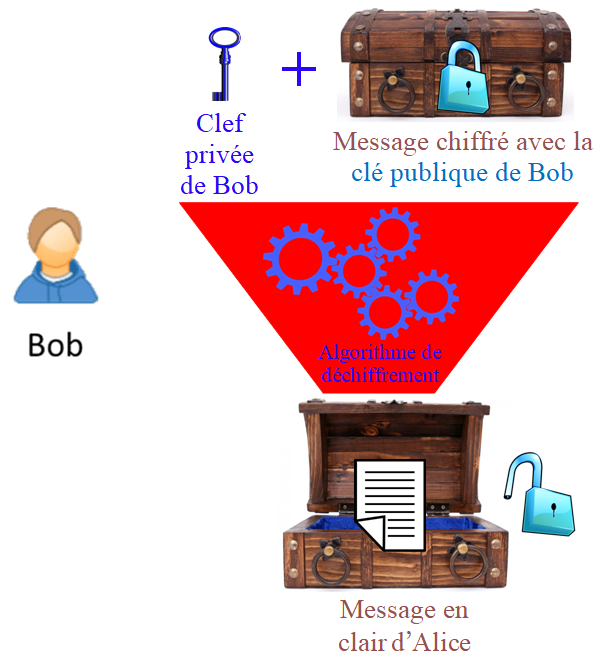
Voici une vidéo pour comprendre le fonctionnement du chiffrement asymétrique :

En reprenant l'analogie cadenas/clé publique, on peut comprendre la sécurité de ce système de chiffrement asymétrique ainsi :

le cadenas ouvert circule initialement ; mais un espion interceptant ce cadenas ouvert n'est pas capable d'en déduire comment ouvrir ce cadenas une fois fermé !
une boîte fermé par un cadenas ; mais un espion interceptant cette boîte n'est pas capable d'ouvrir cette boîte sans la clé conservée par Bob.

Ainsi, ce qui circule est insuffisant pour connaître le message sans une clé privée qui elle ne circule pas.

Tout repose sur le fait qu'il est très facile de fermer un cadenas ouvert mais qu'il est très difficile d'ouvrir un cadenas fermé sans clé.
Dans les chiffrements asymétriques, la sécurité repose sur des problèmes mathématiques de calculs très faciles à résoudre dans un sens mais très difficile à résoudre dans l'autres sens.
L'algorithme RSA permet un chiffrement asymétrique en utilisant le fait :

qu'il est mathématiquement et informatiquement très simple d'effectuer la multiplication de deux nombres (premiers),
qu'il est par contre mathématiquement et informatiquement très compliqué de décomposer un nombre comme produit de deux nombres premiers, sous peu que ces nombres soient suffisamment grands (avec les ordinateurs actuels deux nombres premiers d'au moins 300 décimales).

En fait, il y a une possibilité pour un espion (disons James), d'intercepter le message d'Alice.

Il suffit pour cela que James possède lui aussi son propre cadenas et sa propre clé privée. Il lui "suffit" alors :

James intercepte le cadenas ouvert envoyé par Bob et le remplace par le sien : Alice reçoit donc celui de James en croyant que c'est celui de Bob.
Alice enferme donc le message dans une boîte qu'elle ferme avec le cadenas de James et l'envoie à Bob.
Sauf que James intercepte cet envoi de retour. Avec sa clé privée, il peut ouvrir son propre cadenas, lire (voire modifier !) le message envoyée par Alice puis remettre le message dans la boîte, boîte qu'il referme alors avec le cadenas de Bob qu'il a initialement intercepté ouvert.
Bob reçoit la boîte fermée avec sa propre clé : il peut lire le message (éventuellement modifié !) sans se douter que celui-ci ait pu avoir été lu voire modifié.
De même, Alice ne peut pas se douter qu'elle a utilisé une clé autre que celle de Bob.
James a réussit attaque dite de l'homme du milieu.

En pratique, par exemple dans le protocole HTTPS vu après, l'échange des "cadenas" passe par un tiers de confiance : celui-ci sert d'intermédiaire pour transmettre le "cadenas" et la boîte fermée avec ce cadenas et "certifie", entre autre, l'intégrité du contenu échangé.

Le protocole HTTPS

Après ces lignes difficiles, que diriez-vous d'une petite BD en ligne pour comprendre le protocole HTTPS ?
Si vous êtes intéressé.e.s, n'hésitez pas à visiter ce site ! En plus, il reprend de manière agréable certains points précédents !

Bon, pour ceux qui préférez du texte, reprenons :

Nous avons déjà vu en première que le protocole HTTP (HyperText Transfer Protocol) permet un échange de données entre un client et un serveur, en particulier avec les méthodes GET et POST.
Nous avons déjà vu que ces deux méthodes ne permettaient pas d'assurer la sécurité des communications ; par exemple, un "espion" placé entre le client et le serveur peut observer et récupérer les informations circulant. Cet espion peut ainsi connaître d'éventuelles informations bancaires échangées ou d'autres informations privées !

Dès 1995, le premier navigateur "grand public" Netscape utilisait le protocole SSL (Secure Sockets Layer) pour tenter de sécuriser ces échanges.

Ce protocole a été amélioré à plusieurs reprises pour devenir désormais le protocole SSL/TLS.

Le protocole TLS (Transport Layer Security) est un protocole informatique qui permet de remplir les objectifs de sécurité suivant :

l'authentification du serveur (et du client),
la confidentialité des données échangées grâce à un chiffrement,
l'intégrité des données échangées (assurance qu'elles n'ont pas été modifiées).

Le protocole HTTPS (Hypertext Transfer Protocol Secure) (pour protocole de transfert hypertextuel sécurisé) est la version "sécurisée" du protocole HTTP : une couche chiffrement TLS est rajoutée.

La couche chiffrement du protocole HTTPS se fait en deux temps :

"poignée de main" :
lors de la "poignée de main", l'utilisation d'un chiffrement asymétrique pour vérifier l'authenticité du client et du serveur, pour s'accorder sur la manière de chiffrer la communication ainsi que sur une clé de chiffrement symétrique.
"échange de données" :
à l'issue de la "poignée de main", l'utilisation d'un chiffrement symétrique (le plus souvent le chiffrement AES) en utilisant la clé de chiffrement symétrique obtenue pour chiffrer toutes les données échangées.

Comme un chiffrement asymétrique, puis un symétrique sont utilisés, on parle de chiffrement hybride.

Voici le détail de la première étape, celle de la "poignée de main" (handshake) :

Le client commence par envoyer au serveur une requête HTTPS dans lequel il propose un certains nombres de méthodes de chiffrement que le client peut utiliser pour chiffrer leur communication.
Le serveur répond en renvoyant un certificat assurant son authenticité (assurer par une autorité de certification tierce), en précisant quelle méthode il préfère parmi celles proposées par le client. Le serveur envoie aussi avec le certificat une clé publique (un "cadenas ouvert", la clé privée permettant d'ouvrir ce cadenas reste caché dans le serveur).
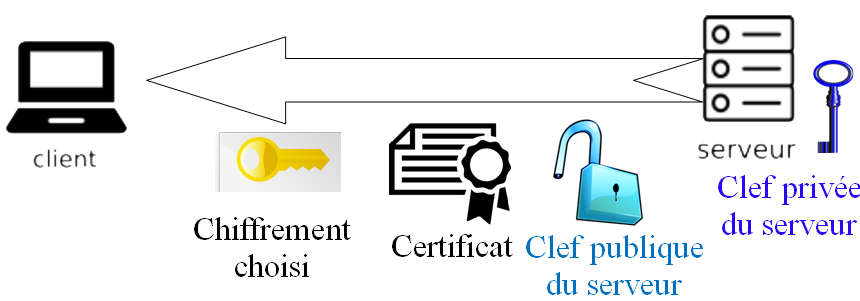
Le client vérifie l'authenticité du serveur grâce au certificat puis crée un code aléatoire qui sera la clé symétrique pour l'échange sécurisé de données. Ce code aléatoire est chiffré grâce à la clé publique du serveur reçu par le client. Le client envoie alors ce code aléatoire chiffré au serveur.
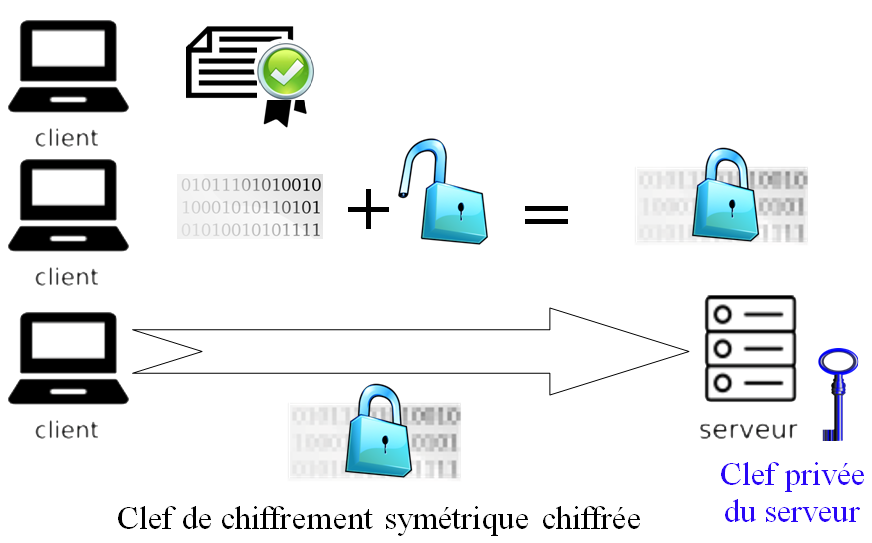
Le serveur utilise sa clé privée pour déchiffrer le message reçu : il accède ainsi au code aléatoire : la clé servant au chiffrement symétrique.

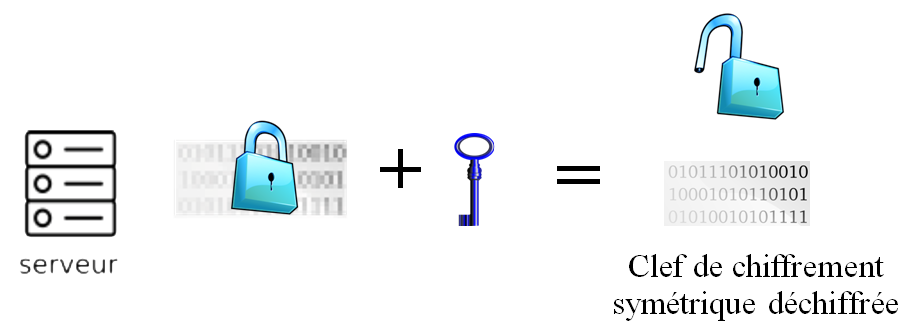
Échange de données.
Cette clé de chiffrement symétrique est ensuite utilisée pour chiffrer tous les contenus dans la communication entre le client et le serveur. Cette clé ne sert que pour une seule session : une autre clé est générée s'il y a déconnexion puis reconnexion.

Exercices issus du bac

Les différents auteurs mettent l'ensemble du site à disposition selon les termes de la licence Creative Commons Attribution - Pas d’Utilisation Commerciale - Partage dans les Mêmes Conditions 4.0 International

▲